Nerdwood.log

고속 역제곱근 알고리즘

 
  • 2025년 09월 11일

고속 역제곱근 알고리즘

쇼츠에서 고속역제곱근 알고리즘 어쩌고 뜨길래 공부해 본 내용. 실무에 쓸 일은 없지만

들어가며

고속 역제곱근 알고리즘은 1/√x 값을 빠르게 근사하는 방법이다.

퀘이크3 아레나에서는 렌더링을 위한 벡터 정규화 연산으로 매 프레임마다 수천 번씩 1/√x 계산이 필요했다. 1990년대에는 GPU가 보편적이지 않았고 CPU의 부동소수점 연산이 느려서 이를 감당하기 어려웠다. 이에 존 카맥이 아래 역제곱근 함수를 작성했고(실제로 만든 건 아님), 이를 본 동료가 감탄하며 “what the fuck?”이라는 주석을 달았다는 일화로 유명해졌다.

float Q_rsqrt( float number )
{
	long i;
	float x2, y;
	const float threehalfs = 1.5F;

	x2 = number * 0.5F;
	y  = number;
	i  = * ( long * ) &y;						// evil floating point bit level hacking
	i  = 0x5f3759df - ( i >> 1 );               // what the fuck?
	y  = * ( float * ) &i;
	y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration
//	y  = y * ( threehalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed
    ...
    
    return y;
}

주요 코드를 한 줄씩 쉽게 설명해보겠다.

단계별 분석

1단계: 타입 펀닝(Type Punning)

i  = * ( long * ) &y;						// evil floating point bit level hacking
  • &y: y가 저장된 메모리 주소
  • (long*): “이 주소에 있는 데이터를 long으로 취급해라”
  • *: long으로 해석된 값을 i에 저장한다.

부동소수점 저장 방식을 떠올려보자.

예를 들어 y = 9.0이 저장되어 있다면 부호는 0(양수)이다. 부동소수점의 정규화에 따라 $9.0 = 2^3 \times 1.125$이므로 지수는 바이어스 127을 더하여 130(10000010)이 된다. 가수는 $1 + 0.125$이고 $0.125 = 2^{-3}$이므로 $1.125 = 1.001_2$가 된다. IEEE754에서 1은 저장하지 않으므로 001(00100000000000000000000)으로 저장된다.

부호(1비트):  |0|
지수(8비트):  |1|0|0|0|0|0|1|0|
가수(23비트): |0|0|1|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|0|

01000001 00010000 00000000 00000000

(long*) 연산은 이 비트 패턴을 정수값으로 해석한다. 결과적으로 변수 i에는 1091567616이 저장된다.

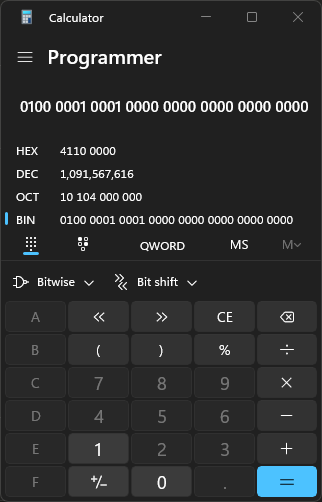
이를 친절하게 설명한 이유는 부동소수점 정규형과 정수 해석 간의 관계를 고려해봐야 하기 때문이다.

부동소수점 정규형 표현:

\[x = (1 + f) \times 2^{e-127}\]

여기서:

  • e: 지수 필드 (8비트)
  • f: 가수부 ($0 \leq f < 1$, 23비트로 표현)

예시: $9.0 = (1 + 0.125) \times 2^{130-127}$

정수 해석 변환:

\[I = e \times 2^{23} + f \times 2^{23}\]

예시: $1091567616 = 130 \times 2^{23} + 0.125 \times 2^{23}$

2단계: 1/√x 계산하기

i  = 0x5f3759df - ( i >> 1 );               // what the fuck?

2.1 로그 변환

1/√x 계산을 위해 로그를 적용하면:

\[\log_2\left(\frac{1}{\sqrt{x}}\right) = \log_2(1) - \log_2(\sqrt{x}) = -\frac{1}{2}\log_2(x)\]

이제 $\log_2(x)$를 효율적으로 계산하는 방법이 필요하다.

2.2 부동소수점에서 로그 추출

부동소수점 정규형 표현에 $\log_2$를 적용하면:

\[x = (1 + f) \times 2^{e-127}\] \[\log_2(x) = \log_2(1+f) + (e-127)\]

$\log_2(1+f)$의 정확한 계산은 테일러 급수를 사용할 수 있지만:

\[\log_2(1+f) = \frac{\ln(1+f)}{\ln(2)} = \frac{f - \frac{f^2}{2} + \frac{f^3}{3} - \cdots}{\ln(2)}\]

이는 고속 계산에 부적합하다. 대신 선형 근사를 사용한다:

\[\log_2(1+f) \approx f + \sigma\]

여기서 $\sigma = 0.0450465$, $f \in [0,1)$ 범위에서 $f$와 $\log_2(1+f)$ 간의 오차값들을 분석하여 평균 오차를 최소화하도록 경험적으로 계산된 보정값이다.

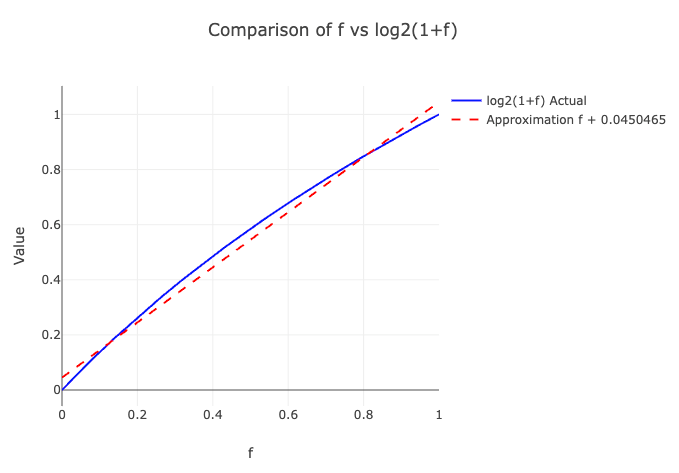
따라서:

\[\log_2(x) \approx f + \sigma + (e-127)\]

2.3 정수 표현과의 연결

정수 해석 변환식에서 $e$를 분리하면:

\[I = e \times 2^{23} + f \times 2^{23}\] \[e = \frac{I}{2^{23}} - f\]

이를 2.2의 결과에 대입하면:

\[\log_2(x) \approx \frac{I}{2^{23}} + \sigma - 127\]

2.4 역제곱근 로그 계산

2.1의 결과를 적용하면:

\[\log_2\left(\frac{1}{\sqrt{x}}\right) = -\frac{1}{2}\log_2(x)\]

2.3의 결과를 대입:

\[\log_2\left(\frac{1}{\sqrt{x}}\right) \approx -\frac{1}{2}\left(\frac{I}{2^{23}} + \sigma - 127\right)\] \[= -\frac{I}{2^{24}} - \frac{\sigma}{2} + 63.5\]

2.5 로그 공간에서 정수 연산으로 변환

로그 공간에서 계산된 $\log_2(1/\sqrt{x}) = -I/2^{24} - \sigma/2 + 63.5$를 정수 연산이 가능한 형태로 변환하는 과정이다.

정수 연산 변환:

2.3에서 도출한 공식을 역으로 정리하면 다음과 같다:

\[\log_2(x) \approx \frac{I}{2^{23}} + \sigma - 127\] \[I \approx (\log_2(x) - \sigma + 127) \times 2^{23}\]

$1/\sqrt{x}$에 적용:

$1/\sqrt{x}$의 정수 표현을 $J$라 하면:

\[J = (\log_2(1/\sqrt{x}) - \sigma + 127) \times 2^{23}\]

2.4의 결과를 대입:

\[J = \left(-\frac{I}{2^{24}} - \frac{\sigma}{2} + 63.5 - \sigma + 127\right) \times 2^{23}\] \[= \left(190.5 - \frac{3\sigma}{2} - \frac{I}{2^{24}}\right) \times 2^{23}\] \[= \left(190.5 - \frac{3\sigma}{2}\right) \times 2^{23} - \frac{I}{2}\]

상수 계산:

$\sigma = 0.0450465$를 대입하면:

\[\left(190.5 - \frac{3 \times 0.0450465}{2}\right) \times 2^{23} = 1597463007\]

이를 16진법으로 표현하면 0x5f3759df이며, 다음과 같이 정리된다.

\[J = \text{0x5f3759df} - \frac{I}{2}\]

i >> 1은 $I/2$ (비트 시프트로 구현된 나누기 2)이므로, 위 수식이 다음 코드로 구현됨을 확인할 수 있다:

i  = 0x5f3759df - ( i >> 1 );

3단계: 뉴턴-랩슨 방법으로 보정하기

y  = y * ( threehalfs - ( x2 * y * y ) );   // 1st iteration

앞서 계산한 근사값의 정밀도를 뉴턴-랩슨 방법으로 개선한다.

뉴턴-랩슨 방법 적용:

$y = \frac{1}{\sqrt{x}}$라면 $y^2 = \frac{1}{x}$이므로 $\frac{1}{y^2} = x$가 성립한다. 따라서 $\frac{1}{\sqrt{x}}$를 구하는 문제는 다음 방정식의 해를 구하는 것과 같다:

\[f(y) = \frac{1}{y^2} - x = 0\]

뉴턴-랩슨 방법의 일반 공식은 다음과 같다:

\[y_{n+1} = y_n - \frac{f(y_n)}{f'(y_n)}\]

$f(y) = \frac{1}{y^2} - x$의 도함수를 구하면:

\[f'(y) = \frac{d}{dy}\left(\frac{1}{y^2} - x\right) = -\frac{2}{y^3}\]

이를 뉴턴-랩슨 공식에 대입하면:

\[y_{n+1} = y_n - \frac{\frac{1}{y_n^2} - x}{-\frac{2}{y_n^3}}\]

분수를 정리하면:

\[y_{n+1} = y_n + \frac{y_n^3 \left(\frac{1}{y_n^2} - x\right)}{2} = y_n + \frac{y_n - xy_n^3}{2}\]

$y_n$으로 묶어내면:

\[y_{n+1} = \frac{y_n}{2}(2 + 1 - xy_n^2) = \frac{y_n}{2}(3 - xy_n^2)\]

최종적으로:

\[y_{n+1} = y_n \times \frac{3 - x y_n^2}{2}\]

코드에서:

코드에서 x2 = x * 0.5이므로 다음과 같다:

\[y_{n+1} = y \times (1.5 - x2 \times y^2)\]

끝맺으며

이 알고리즘은 부동소수점 비트 구조를 정수로 해석하고, 로그 근사를 통해 제곱근 연산을 정수 연산으로 계산하고, 뉴턴-랩슨 방법으로 정밀도를 보정한다. 1990년대 CPU 부동소수점 연산의 성능 한계를 우회하기 위한 방법으로, 현재는 하드웨어 발전으로 실용성을 잃었지만 비트 레벨 최적화 기법을 보여주는 구현으로 한 번쯤 돌아볼 만하다.

검색